I've started a blog on my ongoing beehive monitoring system development and the fist section is mainly about using cheap load cells (about a dollar each) from China. Apologies for not putting it all here but it's only a click away at
http://bugthebees.blogspot.co.uk/

I'd welcome any feedback, on this forum, not under the blog comments. As an inducement to visit the blog here's the curve that says it all really about these devices.

This is really interesting @geo3geo! Nice work.

Would you be interested in collaborating with us? Is this an open source project?

Our electronics developer @mtnscott is doing some amazing work with infrared sensors for our bee counter. Hes already got several temp/humidity sensors active.

Scott - would you be interested to check out Geo's link and assessing? Weight monitoring would be huge!

@trizcs - thanks for the heads up!
@geo3geo - nice work! This is something we would be interested in adding to our sensor monitor. We currently use the Spark Core as it has several advantages over Arduino with integrated WiFi and more SRAM. Seems like you have don some great work on understanding the load cells and their behavior over time. Would you mind posting a link to the cells?

We have an alpha version of our sensor that monitors Temperature in four locations and Humidity in two. Temperature (Inside electronics package, two other locations in the hive and outside) Humidity (inside electronics package and outside). We are currently working on a bee counter for bee activity leaving and entering the hive. Adding a weight sensor would be a great addition to this sensor package. Thanks for sharing!

Did you go thru a lot of weight sensors in your search?

@geo3geo I reviewed your average calculation and you may want to consider changing it. Currently you are calculating the 50 sample average as :
SumOfSamples = SumOfSamples - SumOfSamples/50 + NewReading
I think you will build up an error over time as you add the real measurement but only subtract an average measurement.

Another solution would be to keep all 50 values. If you normalize the data to byte (0-255) it will only take 55 bytes.

byte *_p;                       // pointer to cell in _load
bool _bMovingAverageStart;      // initialization flag on moving average
byte _load[50];                 // moving average array of data points
int SumOfSamples;               // moving average

void setup {
    // your code

    // initialize the moving average array
    _pMovingAverageStart = true;
    _p = _load;
    *_p = NormalizedNewReading;
    SumOfSamples = *_p++;
}

void loop {
    // your code

    // test if we are rolling over the buffer
    if ( (_p - _load) >= sizeof(_load) ) {
        _bMovingAverageStart = false;
        _p = _load;
    }

    // subtract the 50th previous entry, unless we are initializing the array
    if (!_bMovingAverageStart)
        SumOfSamples -= *_p;

    // save the new value
    *_p = NormalizedNewReading;

    // add the new reading to the rolling sum
    SumOfSamples += *_p++;

    // calculate the moving average
    if (!_bMovingAverageStart)
        MovingAverage = SumOfSamples / 50;
    else
        MovingAverage = SumOfSamples / (_p - _load);

}

I'm writing this on the fly so I can't guarantee it works. The basic logic is to setup a buffer that rolls over to the beginning when we reach the end. Then with each new sample subtract the value in the buffer at the current pointer (50 reads ago) from your rolling sum then store the new reading in the buffer (replacing the one from 50 reads ago), next add the new reading to the rolling sum and increment your pointer in the buffer. Then just divide the rolling sum by 50 and you have your moving average.

Hope this helps.

Hi Trizcs - I thought I was collaborating in a way, simply by putting my load cell info up for comment. Or is a bit more formal than that? No doubt I've missed something.

Hi mtnscott
You raise some interesting points, I'll take them as they come.

1. Actually I simplified things a bit in my blog, I'm not really using an Arduino as such, but a Sweetpea LeoFi which is a Leonardo Arduino with built-in TI CC3000 wifi controller (just like the Spark!) Only problem is, the wifi libraries (from Adafruit) don't leave enough space for my program. The Swedish sweetpea designer is about to release their own, much smaller, library called tinyhci but so far it hasn't appeared. I'm in contact with them and they said I'd have something at the end of last week but sadly, nothing yet. The LeoFi only has 32Kb flash, looks like the Spark has 128Kb, a mega advantage. I'll look into it further in case I have to abandon the Sweetpea ship. If Sweetpea happens it'll make for a very low cost and very neat package. I wasn't going to mention it in my blog til I knew which way I was going. If there's more info about on the Spark packaging, esp Arduino connectivity, I'd appreciate any links etc. Seems much of it isn't available til 2015 (?).

2. Load cell eBay link is http://www.ebay.co.uk/itm/4pcs-Body-Load-Cell-Weigh-Sensor-Resistance-strain-Half-bridge-sensors-50kg-/181284138618?pt=UK_BOI_Electrical_Test_Measurement_Equipment_ET&hash=item2a35606e7a

3. I'd already clocked the IR bee counter project, sounds great fun. I wondered about ultrasonics as a rough way of measuring volume of traffic. I've been playing around with these sensors and they seem pretty sensitive. Can't count bees with it obviously.

4. No, didn't investigate other load cells. Just found something on eBay that looked promising and went to work on it. Actually I've just started another test run on my sensors, now with modified software to compensate for temperature. This is a good time of year as overnight temps are low here - I have the kit in an unheated conservatory and log results early morning and midday to get a good spread of results.

5. Regarding the averaging, I did actually start with something similar to what you suggest but wanted something a bit more compact. My one line of code is certainly compact! I did ponder whether it was giving a true average and I'm still not sure. Can't get my head round it somehow. What I'll do when I get a few hours spare is write a bit of software, under Processing as it's more convenient, to do the following
   a. generate a set of numbers with random variation
   b. feed the same numbers through both algorithms (yours and mine)
   c. plot the two resultant averages against time
   Should be interesting!

As I can't get my kit online yet I'm actually monitoring the hive weight on a weekly basis using a somewhat older form of technology - bathroom scales! Surprisingly easy and useful. I also have a simple temp probe with digital readout monitoring the brood chamber. So I'm keeping an eye on them.

Also, I've added a few photos of my packaged bee monitor to my blog. You may like to have a look.

Thanks for the feedback - nice to be able to exchange ideas in this way
Geo

This is a follow-on posting. I've produced the Processing software to check out the two averaging algorithms and the program is up there on the web at http://www.openprocessing.org/sketch/175334
It should be interactive, I got a bit carried away with it, allowing different sample size and noise levels using the f/F and n/N keys but on the Openprocessing site this doesn't work, something to do with it being a Javascript version, to get the fully interactive version simply copy and paste the code into your Processing IDE. It's worth doing as it's revealing to see the effects of changing sample size for different noise levels.

Anyway the bottom line is that the 'long' algorithm (red) responds much quicker to changes in load cell than the 'short' algorithm (green). However both do much the same job of filtering out noise, and there is no error build up using the 'short' version. If anything the 'short' version filters a bit better, after all it is slower to respond to variations in input signal. For the load cell, as changes are very slow and response time is not an issue, I think I'll be sticking with the short version.

One thing I can't figure is why, on the curve shown which is for filtering over 20 samples, it takes 40 samples for the red curve to hit its average. If anyone can see an error in the code I'd appreciate knowing where it is! Anyway it doesn't detract from the general conclusion.

Geo

New processing sketch uploaded to correct the software bug referred to above. I've uploaded in Java rather than javascript this time so the keyboard interaction now works too!

http://openprocessing.org/sketch/175694

Geo

@geo3geo Sorry for the delayed reply. You can find more info on the Spark Core here Spark - Hackable WiFi Module It comes with 128MB of flash however about ~75K is consumed for the core firmware. The next generation Photon will address this with much more flash. I like having the 20K of SRAM. I'll take a look at your processing work. From a quick glance it looks like there is no error build up. That's good. Thanks!

A further test run on the load cells, now with temp compensation n software, is far more encouraging. The curve below is over 5 days and shows quite a stable situation. Ingore the first reading, I added that one to force the scaling, making it similar to previous plots.

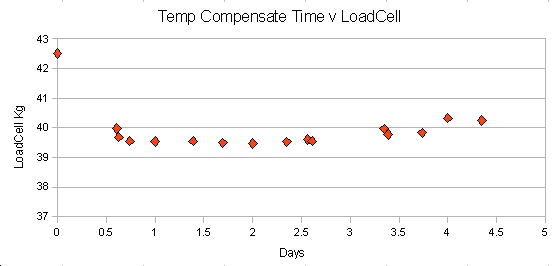
I'm beginning to wonder if there was some other factor that crept in to the previous test run. Anyway I'm more than happy with the cells for now and am moving on to do on-line tests inputting data into Plotly. I've had to make a lot of changes and compromises to get my code into the small amount of flash memory after the Adafruit and Plotly libs are included, but I have something that's looking promising at last. Plot is of two temps and weight (in red) - test environment for now, not a real hive yet but getting very close.

Oh yes, and I've added a hardware watchdog to get over issues with the Adafruit/Plotly library functions hanging up every few hours. But good progress! If anyone has a cut down version of the adafruit_cc3000 library files I'd be very interested!

UPDATE

I've posted an update to my blog at bugthebees.blogspot.co.uk
The evidence is that the cells are NOT SUITABLE for continuous beehive monitoring. But as always there is a way around the problem!

Read the blog for details/curves/ideas etc.

Geo

Hey,
there seems to be some good research (german language) out there already on well performing load cells with arduino integration.
They are suggesting an Aluminium block design with loads up to 100-500kg. The accuracy with one of the tests has been +-15grams. Pretty accurate!
Costs are quite a bit more: about 35€/unit.
Here's the link to the product:
http://www.bosche.eu/produkte/waegezellen/plattform-waegezellen-h40a
and here's the way you use it to measure weight:

I would like to go into some tests with these sensors so we can collaborate with hiveeyes.org.

I opened a new Thread concerning the issue how we actually are able to install a load cell into the hive designs.

That's brilliant! I think 35e is great value for the accuracy. I'll be following this up.

I'll take this opportunity to give a brief update on my own load cell issue. There's a new entry at my
http://bugthebees.blogspot.co.uk/ which explains my interim solution of manually lowering the hive onto the cells when I need a reading. Not ideal but it works!

View ongoing real-time data for Hive #1 at www.mecol.co.uk/P11.php

@geo3geo Hi Geo3geo, I am trying to make cheap bee hive scale. I am using same sensors you tried fristly, cheap sensors from ebay, not parallel beam single point(your second choise). I would like to now if you are sure about positioning sensorload cell mounting. I positioned it on the opposite side, so it rests on two bolts. I know it works either way, but which is more proper?
thanks! this blog is helpfull:)

Hi Zack.
I'm sorry but I can't really understand the question. A sketch or photo would help.
However in my opinion the low cost cells are really a waste of time, too much drift when on constant load. The Bosch cells are not that expensive really and work very well. See results at my beeblog15.blogspot.com

regards
Geo

I want to thank you, Geo for the great research and testing of the cheap load cells! I found similar like you have used at Sparkfun and I was on the verge of testing this out. The charming side is the frame building. You need only a board and put the load cells on each corner.

Experimenting with single point load cells is more challenging. The load cell posted from Ron was first tested on my desk, I was glad that Markus had some welding skills and he got the frame working.

I tried out a kind of box for mounting the load cell under a hive, see https://www.facebook.com/cgruber.de/media_set?set=a.10201453236152539.1073741827.1224510416&type=1&l=bca3f242ae

A more easy way--for the frame-- is mounting the load cell only under the half of a floorboard and take the measurement twice as Geo did in the second approach or LegoLars in this posting http://forum.arduino.cc/index.php?topic=113534.msg1473176#msg1473176

I will try this also with a load cell, two distance plates and two alloy L-profiles.

You have done really a good job. I like your post. Thanks for the informative post